|
2018-02-11 23:02
조회: 17,198
추천: 20
SS쥬얼링에 사용되는 비용의 수학적 추정방법SS쥬얼링에 사용되는 비용의 수학적 추정 1. 서론 1) 목적 저번에 코인이 남는 관계로 SS쥬얼링을 맞춰보고자 C급 보석들을 절구에 돌렸는데, 5만원을 요구하는 것에 대해 본인은 매우 깜짝 놀랐다. 조합비용이 있는줄 몰랐던 것이였다. 그리하여 본 보고서는 SS쥬얼링까지 가는데 필요한 비용을 수학적인 방법으로 추정하여 비용을 알아내고자 한다. 2) 연구방법론 확률과 수학을 사용한다. 문과여서 자신이 없다. 2. 본론 1) C->B 변환까지 드는 비용의 추정 우선, 우리는 C보석의 갯수가 최소 2개부터 최대 250개까지라는 것을 알 수 있다. 이는 이벤트 기간을 계산하였을때, 박스를 총 250개 얻을 수 있기 때문이다. 하지만 여기서는 각 유저들이 정확한 갯수를 알 수 없다고 판단하였기 때문에, 갯수를 k라는 미지수로 둔다. 그리고 하루에 유저들이 박스 10개를 산다는 가정을 추가한다.(그리하여, k는 10개부터 250개 까지의 자연수) 그리고 조합 비용은 C->B까지 가는데 횟수당 5만원이지만, 여기서는 그 비용의 유동성을 고려하여 x라는 미지수로 둔다.(x는 자연수) 자, 이제 본격적으로 수학적인 추론을 하자면 다음과 같다. 우리는 k개를 가지고 있다면. [k/2]번을 돌릴 수 있을 것이다. 여기서 왜 'k/2'가 아니라 '[k/2]'인 이유는, 2개 단위로만 돌릴 수 있기 때문에, 횟수에서 홀수가 나오는 경우는 어짜피 2를 나누기에 소수점을 버리면 된다고 생각하였기 때문이다.(가우스) 그리고 C->B의 성공확률은 70%이기에 7k/20개를 얻을 수 있고, 반대로 3k/20개가 실패하여 남게 된다. 결국 k개를 전부 돌린다면, 3k/20개가 남게 된다. 하지만, 여기서부터 문제가 발생하게 되는데, 만약 홀수개가 남게 된다면, 우리는 다음에 돌릴 횟수에서 1개를 빼주어야 한다. 이는 2개 단위로 돌릴 수 있기 때문이다. 그리하여 k가 10 이상일 때, 각 영역에서는 다음 횟수는 [0.5*(0.3k-1)]이 되고, 이 횟수가 가장 적은 상태의 횟수이다. 반대로 가장 많은 횟수는 [0.5*0.3k]라고 할 수 있다. 이제 이것을 돌리면, 홀수일 경우에는 [0.3*0.5*(0.3k-1)]개가 다시 남게 된다.(짝수는 [0.3*0.5*0.3k]) 그리고 k가 26보다 큰 경우(C급 보석이 26개 이상인 경우)에는 다시 돌릴 수 있기 때문에, 다음 횟수는 홀수일 경우 0.5*(0.5*0.3*(0.3k-1)-1)이 되고, 짝수일 경우에 k가 23보다 클 때는, (0.5*0.3)^2*k가 된다. 마지막으로, k가 90보다 큰 경우(C급 보석이 90개 이상인 경우)에는 또 다시 돌릴 수 있기 때문에(4번째 돌려버리기~), 다음 횟수는 홀수일 경우 0.5*(0.5*0.3(0.5*0.3(0.3k-1)-1)-1)이 되고, 짝수일 경우에 k가 150보다 클 때는, (0.5*0.3)^3*k가 된다. 결국, 계속 돌릴 때, 전부 홀수 개가 나오는, 가장 작은 경우부터 시작하여 전부 짝수 개가 나오는, 가장 큰 경우까지 대략적으로 평균을 잡은 식은 다음과 같다.(경우의 수에 따라 식이 전부 다르기에 가장 작은것과 가장 큰 것을 더하여 2로 나누었다. 이는 중심극한정리에 따라서 가장 가깝게 나오는 값이기도 하며, 본인이 일일이 경우의 수를 전부 계산하면서 식을 만들기에는 한계가 있기 때문이다 ㅠㅠ)
그리고 여담이지만, 사실 여기까지 보는 사람도 없을 것이라고 예상한다. 옛날 인소야때도 그랬으니깐.. ㅠ (다읽으면 칭찬드림) 그래서 이해용 그림은 지금 안올리고 나중에 올릴 생각이다. 귀찮다. 2) B->A변환까지 드는 비용의 추정 다음으로, C->B 변환이 끝난 경우, 70%확률로 B급 보석이 생겼을 것이다. 이 B급 보석을 A급 보석으로 만들때 들어가는 비용을 다시 추정하고자 한다. 당연히 2-1의 방법과 동일하다고 보면 된다. 다만, 여기서는 보석의 갯수를 m으로 표현한다. 이는 B급 보석의 성공확률을 고려하면, B급 보석은 7k/20개가 나오기 때문이다. 그리고 보석의 수는 자연수가 되어야 하기 때문에 가우스를 사용한다. 따라서 [7k/20]=m이다.(간단하게 표현한 것) 당연히 위의 방법처럼 할 경우 다음과 같은 식이 나온다.
3) A->S변환까지 드는 비용의 추정 다음으로, B->A 변환이 끝난 경우, 50%확률로 A급 보석이 생겻을 것이다. 이 A급 보석을 S급 보석으로 만들때 들어가는 비용을 다시 추정하고자 한다. 당연히 2-1의 방법과 동일하다고 보면 된다. 다만, 여기서는 보석의 갯수를 n으로 표현한다. 이는 A급 보석의 성공확률르 고려하면, A급 보석은 7k/80 (m/4)개가 나오기 때문이다. 그리고 보석의 수는 자연수가 되어야 하기 때문에 가우스를 사용한다. 따라서 [7k/80]=[m/4]=n이다.(간단하게 표현한 것) 당연히 위의 방법처럼 할 경우 다음과 같은 식이 나온다.
4) S->SS변환까지 드는 비용의 추정
2000만원이라 카더라. 3. 결론 결국, C급 보석을 통해 SS쥬얼링을 만들기 위해서는 다음과 같은 비용이 들어간다는 것을 수학적으로 알 수 있다. 따라서 SS쥬얼링을 만들기 위해 들어가는 총 비용함수를 "F"라 하면...
이 된다. 하지만 실제로 저기다가 숫자를 넣어서 계산하기란 불가능에 가깝다고 생각한다. 그리하여! 본인은 '엑셀'을 준비하였다. 첨부파일에 계산을 위한 엑셀파일을 실어두었다.(편리성~) 4. 연구의 한계 여기서는 많은 한계가 존재한다. 첫 번째 한계는, 쥬얼 박스를 오픈할 경우 C급 보석만 뜬다고 가정하였기 때문이다. 두 번째는 C(x,k)함수와 A(x,n)함수는 k와 n값이 얼마냐에 따라서 정확한 식이 다르다. 여기서는 본인이 계산을 단순하게 하기 위해(응?) C(x,k)함수와 A(x,n)함수의 범위값만 구하였다.
EXP
1,432
(16%)
/ 1,601
경매장 및 이벤트 탐색 (모노모, 캡틴, 268) <<공개데이터DB>> ㅁ 경매장API머신러닝 ㅁ 경매장측정방법론 - 경매장 시세탭의 일부 패턴 정리(추천): https://www.inven.co.kr/board/maple/2304/31625 ㅁ 오로라경매장 소비템, 기타템 분야 ㅁ 오로라경매장 드메템 - 2023년 1분기 드메템 통계: https://www.inven.co.kr/board/maple/5974/1210032?my=post - 2023년 2분기 드메템 통계: https://www.inven.co.kr/board/maple/2304/34596?my=post - 드메템 가격 총괄분석(하프이어링): https://www.inven.co.kr/board/maple/2299/8787209?my=post - 드메템 가격 총괄분석(얼장): https://www.inven.co.kr/board/maple/2299/8794254?my=post - 드메 상대적 효율 분석: https://www.inven.co.kr/board/maple/2299/7396474?my=post ㅁ 오로라경매장 시드링 - 2023년 7~9월 시드링 추세: https://www.inven.co.kr/board/maple/2304/35612?my=post ㅁ 메포 시계열 - 월말: https://www.inven.co.kr/board/maple/2304/30089?my=post
|
인포메이션
명칭: 주식회사 인벤 | 등록번호: 경기 아51514 |
등록연월일: 2009. 12. 14 | 제호: 인벤(INVEN)
발행인: 박규상 | 편집인: 강민우 |
발행소: 경기도 성남시 분당구 구미로 9번길 3-4 한국빌딩 3층
발행연월일: 2004 11. 11 |
전화번호: 02 - 6393 - 7700 | E-mail: help@inven.co.kr
인벤의 콘텐츠 및 기사는 저작권법의 보호를 받으므로, 무단 전재, 복사, 배포 등을 금합니다.
Copyrightⓒ Inven. All rights reserved.
인터넷 신문 위원회 배너
2023.08.26 ~ 2026.08.25
인벤 온라인서비스 운영
(웹진, 커뮤니티, 마켓인벤)
▲
(주)인벤 사업자등록번호 : 120-86-74756
대표전화 : 02-6393-7700
FAX : 02-6393-7706
인벤의 콘텐츠 및 기사는 저작권법의 보호를 받으므로, 무단 전재·복사·배포 등을 금합니다.
Copyright © Inven Communications. All rights reserved.
대표전화 : 02-6393-7700
FAX : 02-6393-7706
인벤의 콘텐츠 및 기사는 저작권법의 보호를 받으므로, 무단 전재·복사·배포 등을 금합니다.
Copyright © Inven Communications. All rights reserved.


 c14366339562.zip [9Kb]
c14366339562.zip [9Kb]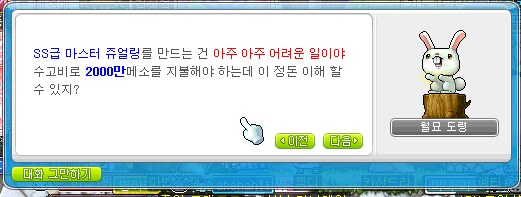
 Staregg
Staregg 










