|
2014-07-01 18:18
мЎ°нҡҢ: 8,602
추мІң: 13
нҶөкі„м ҒмңјлЎң кі„мӮ°н•ҙліё к·ёл Ҳмқҙл“ңмһ‘мқҳ мӣҗк°Җл“Өм–ҙк°Җкё°м—җ м•һм„ң..
В
мӮ¬лһҢл“Өмқҙ нҶөкі„м—җ лҢҖн•ҙ н–Үк°Ҳл Өн•ҳлҠ” кІғ В мқјлӢЁ к°„лӢЁн•ң мҳҲл¶Җн„° н•ҳлӮҳ л“Өм–ҙліҙкІ мҠөлӢҲлӢӨ. 2лҢҖмқҳ кІҪмҳӨк°Өмқҙ мһҲмҠөлӢҲлӢӨ. мҰқм„ңлҠ” 100м–өмқҙлқјкі м№ҳмЈ . лӘ©н‘ңлҠ” м—¬кё°м—җ к°Җк°•1,2лҘј л¶ҷм—¬м„ң нҢҢлҠ” кІҒлӢҲлӢӨ. к·ёлҹ°лҚ° н•ҳлӮҳлҠ” лӢЁ 10м–өм—җ к°Җк°• 1,2к°Җ л¶ҷм—Ҳкі лӮҳлЁём§Җ н•ңлҢҖлҠ” мҡҙмқҙ м—Ҷм–ҙм„ң 50м–өмқ„ л“Өм—¬м„ң к°Җк°• 1,2к°Җ л¶ҷм—Ҳл„Өмҡ”. к·ёл ҮлӢӨл©ҙ мқҙ кІҪмҳӨк°Өл“Өмқҳ мӣҗк°ҖлҠ” м–јл§Ҳмқјк№Ңмҡ”? к°„лӢЁн•ҳмЈ .. к°Ғ ((100+10)м–ө + (100+50)м–ө )/ 2 = 130 м–өмһ…лӢҲлӢӨ. мҰү к°Җк°• 1,2мқҳ к·ёл Ҳмқҙл“ң мӣҗк°ҖлҠ” 30м–өмқҙкө°мҡ”.. к·ёлҹ¬лӮҳ лӢЁ 2лҢҖл§ҢмңјлЎң кІҪмҳӨк°Өмқҳ к·ёл Ҳмқҙл“ң мӣҗк°ҖлҘј кі„мӮ°н•ҙ лӮҙлҠ”кұҙ лӯ”к°Җ 비м•Ҫмқҙ мӢ¬н•ҳлӢӨкі мғқк°Ғлҗ©лӢҲлӢӨ. л§һм•„мҡ” кё°ліём ҒмңјлЎң нҶөкі„н•ҷмқҖ "л¬ҙмҲҳнһҲ л§ҺмқҖ" н‘ңліёмқҖ "к·ё нҷ•лҘ 분нҸ¬"лҘј л”°лқјк°„лӢӨлҠ” м „м ңм—җм„ң мӢңмһ‘н•ҳкұ°л“ мҡ”. лӢЁ 2лҢҖмқҳ н‘ңліёмқҖ л¬ҙмҲҳнһҲ л§ҺлӢӨкі н• мҲҳ м—ҶмңјлҜҖлЎң мң„ к°ҖкІ©мқ„ мӣҗк°Җлқјкі мұ…м •н• мҲҳ м—ҶмҠөлӢҲлӢӨ. к·ёл ҮлӢӨл©ҙ мўҖ лҚ” нҳ„мӢӨм ҒмңјлЎң кІҪмҳӨк°Өмқҙ 50мІҷмқҙ мһҲмҠөлӢҲлӢӨ. к·ёлҹј мқҙл•Ңм—җлҸ„ к°Ғк°Ғ кІҪмҳӨк°Өм—җ к°Җк°•1,2к°Җ л¶ҷлҠ” к°ҖкІ©мқ„ кі„мӮ°н•ҳкі В к·ё к°ҖкІ©мқ„ лӘЁл‘җ лҚ”н•ҙм„ң нҸүк· мқ„ лӮҙл©ҙ, мқҙ л…Җм„қл“Өмқҳ нҸүк· к°ҖкІ©мқ„ лӮҙл©ҙ мўҖ лҚ” м •нҷ•н•ң к°ҖкІ©мқ„ мұ…м • н• мҲҳ мһҲкІ кө°мҡ”.. к·ёлҹј л§Ңм•Ҫм—җ мҲҳл§ҢмІҷ(!) мқҳ кІҪмҳӨк°Өмқ„ к°Җм§Җкі мһҲлӢӨл©ҙ(мқҙкұё м •нҷ•н•ҳкІҢлҠ” "emsemble:м•ҷмғҒлё”"мқҙлқјкі л¶ҖлҰ…лӢҲлӢӨ.) В мқҙ л…Җм„қл“Өмқ„ лӘЁл‘җ к°Җк°•12 л¶ҷмқҙлҠ”лҚ°м—җ л“ңлҠ” 비мҡ©мқ„ кі„мӮ°н•ҳл©ҙ м •нҷ•н•ң мӣҗк°ҖлҘј кі„мӮ°н•ҙ лӮј мҲҳ мһҲмҠөлӢҲлӢӨ. к·ёлҹ¬лӮҳ! мӢӨм ңм ҒмңјлЎң мҲҳл§ҢмІҷмқҳ кІҪмҳӨк°Өмқ„ лӘЁл‘җк°•нҷ”н•ҳлҠ”кұҙ л¬ҙлҰ¬мһ…лӢҲлӢӨ. кІҢлӢӨк°Җ м–ҙл–Ө л…Җм„қл“ӨмқҖ (нҷ•лҘ мқҙ 0мқҙ м•„лӢҲлҜҖлЎң) мҲҳмӢӯ мҲҳл°ұлІҲ к°•нҷ”н•ҙлҸ„ мҳҒмӣҗнһҲ к°Җк°• 12к°Җ л¶ҷм§Җ м•ҠлҠ” кІҪмҡ°к°Җ мЎҙмһ¬н•ҳкІ м§Җмҡ”...(м•„л§Ҳ лӮң м•Ҳлҗ кәјм•ј..) л”°лқјм„ң мқҙлҹ° л¬ҙн•ңн•ң кІҪмҡ°мқҳ 분нҸ¬(x 축мңјлЎң л¬ҙн•ң -infinity)н•ҳлӢӨл©ҙ к·ёлғҘ мҡ°лҰ¬к°Җ м•„лҠ” кё°лҢҖк°’ нҷ•лҘ лЎң кі„мӮ°н•ҙм„ңлҠ” м•Ҳлҗ©лӢҲлӢӨ. мҰү нҷ•лҘ 분нҸ¬лҘј м Ғ분н•ҙм„ң м •к·ңнҷ”(nomalized) мӢңнӮЁлӢӨмқҢ мӣҗн•ҳлҠ” кө¬к°„мқ„ м Ғ분н•ҙм„ң нҷ•лҘ мқ„ м•Ңм•„лӮҙм•ј м •нҷ•н•ң к°’мқҙ лҗҳлҠ”кұ°мЈ .. л„Ҳл¬ҙ мқҙлЎ м Ғмқҙлқјм„ң мң„ кёҖмқҙ мқҙн•ҙм•Ҳк°ҖмӢ лӢӨл©ҙ, м ңк°Җ кёҖмқ„ лӘ»мҚЁм„ң к·ёлҹ°кұ°м§Җ, мқҙ кёҖмқ„ мқҪлҠ” 분мқҙ мһҳлӘ»лҗңкІҢ м•„лӢҷлӢҲлӢӨ. м•„л¬ҙнҠј м•„лһҳлЎң л„ҳм–ҙк°ҖлҸ„лЎқ н•ҳм§Җмҡ” :) к·ёлҹј лҢҖн•ӯн•ҙмӢңлҢҖ к·ёл Ҳмқҙл“ңм—җ м Ғмҡ©н•ҙліҙл©ҙ.. В лҰ¬лІ„мҠӨм—”м§ҖлӢҲм–ҙл§ҒмқҙлһҖ, мҷ„м„ұлҗң мөңмў… нҳ•нғңмқҳ м ңн’Ҳмқ„ 분м„қн•ҳм—¬ м ңн’Ҳмқҳ кё°ліём Ғмқё м„Өкі„ к°ңл…җкіј м Ғмҡ©кё°мҲ мқ„ нҢҢм•…н•ҳкі мһ¬нҳ„н•ҳлҠ” кІғмһ…лӢҲлӢӨ. н”„лЎңк·ёлһЁмқҳ кІҪмҡ°лқјл©ҙ, мҷ„м„ұлҗң н”„лЎңк·ёлһЁмқҳ кІ°кіјлҘј к°Җм§Җкі мң 추н•ҳм—¬ н”„лЎңк·ёлһЁмқҳ кө¬мЎ°м Ғ кө¬нҳ„ мӣҗлҰ¬, мҰү м•Ңкі лҰ¬мҰҳмқ„ 추측н•ҳлҠ” кІғмқҙкІ м§Җмҡ”. к·ёлҹ¬лӮҳ мқҙкІҢ кІ°мҪ” мүҪм§Җ м•ҠмҠөлӢҲлӢӨ.м—¬лҹ¬к°ңмқҳ н•ЁмҲҳк°Җ мӮ¬мҡ©лҗҳкі мһҲлҠ” н”„лЎңк·ёлһЁм—җм„ң к·ё м•Ңкі лҰ¬мҰҳмқ„ м •нҷ•нһҲ мң 추н•ҙлӮҙлҠ” кІғмқҖ л§Өмҡ° м–ҙл Өмҡёлҝҗ лҚ”лҹ¬, кұ°кё°м—җ мӢ¬м§Җм–ҙ лӮңмҲҳ(Random)к°’к№Ңм§Җ нҸ¬н•Ёлҗҳм–ҙмһҲлӢӨл©ҙ, м •нҷ•н•ң кө¬лҸҷмӣҗлҰ¬лҠ” м•Ңм•„лӮҙлҠ”кІғмқҖ л¶Ҳк°ҖлҠҘм—җ к°Җк№қм§Җмҡ”. В лһңлҚҳмҠӨнӮ¬мқҙ л¶ҷлҠ” к·ёл Ҳмқҙл“ң мһ‘м—… м—ӯмӢң л§Ҳм°¬к°Җм§Җмһ…лӢҲлӢӨ. мҲҳл§ҺмқҖ м—¬лҹ¬к°Җм§Җ ліҖмҲҳ(Parameter)к°Җ ліөн•©м ҒмңјлЎң мһ‘мҡ©н•ҳлҠ” л§ҢнҒј (кІҢлӢӨк°Җ кұ°кё°м—җ нҷ•лҘ мқҙ нҸ¬н•Ёлҗҳм–ҙмһҲлҠ” мқҙмғҒ)лӢӨмқҢм—җ л¶ҷмқ„ мҠӨнӮ¬мқ„ нҷ•мӢӨнһҲ мҳҲмёЎн•ҳкі кі„мӮ°н•ҙлӮҙлҠ”кұҙ м ңмһ‘мһҗк°Җ м•„лӢҢмқҙмғҒмқҖ л¶Ҳк°ҖлҠҘн•©лӢҲлӢӨ. к°ҷмқҖ мқҙмң лЎң лӮҙк°Җ к°Җк°•1, 2 к°ңмЎ°лЎұмқҙ к°Җм§Җкі мӢ¶лӢӨкі н• л•Ңм—җ, м •нҷ•нһҲ к·ёл Ҳмқҙл“ңмһ‘м—…м—җ м–јл§ҲлҘј мҸҹм•„л¶Җм–ҙм•ј мң„мҷҖ к°ҷмқҖ мҳөм…ҳмқ„ к°Җм§Җкі мһҲлҠ” к°ңмЎ°лЎұмқ„ кө¬н• мҲҳ мһҲлҠ”м§Җ мҡҙмҳҒмһҗк°Җ м•„лӢҢ мқҙмғҒм—җм•ј м•Ң мҲҳ м—Ҷм§Җмҡ”.(м–ҙм©Ңл©ҙ мҡҙмҳҒмһҗлҸ„ м•Ң мҲҳ м—Ҷм§Җмҡ”..) лӢӨл§Ң..В к·ёлҹ¬лӮҳ мң м Җ мһ…мһҘм—җм„ңлҸ„ м–ҙлҠҗм •лҸ„ к·ё кі„мӮ°кіјм •мқ„ мң 추н•ҳкі лҢҖлһөм Ғмқё мҳҲмғҒ кё°лҢҖк°ҖкІ©мқ„ мӮ°м¶ңн•ҙ лӮј мҲҳ мһҲлҠ”лҚ°, л°”лЎң 충분н•ң н‘ңліёмқ„ нҶөн•ҙм„ң мӢӨн—ҳмқ„ н•ҳлҠ” кІғмқҙмЈ . к·ёл Ҳмқҙл“ң мһ‘м—…м—җ л“Өм–ҙк°ҖлҠ” 비мҡ©
к·ёл ҮлӢӨл©ҙ мқјлӢЁ к·ёл Ҳмқҙл“ң мһ‘м—… мһҗмІҙм—җ л“Өм–ҙк°ҖлҠ” 비мҡ©мқ„ кі„мӮ°н•ҙлҙ…мӢңлӢӨ. В мһ‘업비мҡ© В = В (((1м§Җ) * ((N_1 * н•Ёмһ¬кё°)+1)) + (2м§Җ) + (3м§Җ)) * ((N_2 *н•Ёмһ¬кё°)+1))В
м—¬кё°м„ң 1м§Җ, 2м§Җ, 3м§ҖлҠ” к°Ғк°Ғ 1к·ёл Ҳмқҙл“ң, 2к·ёл Ҳмқҙл“ң, 3к·ёл Ҳмқҙл“ңлҘј к°Ғк°Ғ н• л•Ң л“ңлҠ” 비мҡ©мһ…лӢҲлӢӨ. к·ёлҰ¬кі N_1мқҖ 1мҠӨнӮ¬м—җм„ң лҜёлҒ„лҹ¬м§„ нҡҹмҲҳ, N_2лҠ” л‘җлІҲм§ёмҠӨнӮ¬(мҰү 3к·ёл Ҳмқҙл“ң ліҙл„ҲмҠӨ)м—җм„ң лҜёлҒ„лҹ¬м§„ нҡҹмҲҳмқҙм§Җмҡ”. мҰү мІ«лІҲм§ё мҠӨнӮ¬м—җлҸ„ л§ҲмқҢм—җ л“ңлҠ” мҠӨнӮ¬мқҙ л¶ҷкі , л‘җлІҲм§ё мҠӨнӮ¬м—җлҸ„ л§ҲмқҢм—җ л“ңлҠ” мҠӨнӮ¬мқҙ н•ңлІҲм—җ л¶ҷлҠ”лӢӨл©ҙ(мҰү к·ёл Ҳмқҙл“ңк°Җ н•ңлІҲм—җ м„ұкіөн•ңлӢӨл©ҙ) мһ‘업비мҡ©мқҖ м•„лһҳмҷҖ к°ҷмқҙ лӢЁмҲңнҷ” лҗ кІғмһ…лӢҲлӢӨ. В мһ‘업비мҡ© = 1м§Җ + 2м§Җ + 3м§Җ
к·ёлҹ¬лӮҳ 1м§Җм—җ л§ҲмқҢм—җ л“ңлҠ” мҠӨнӮ¬мқҙ л¶ҷлҚ”лқјлҸ„, 3м§Җм—җ мӣҗн•ҳм§Җ м•ҠлҠ” мҠӨнӮ¬мқҙ л¶ҷлҠ”лӢӨл©ҙ м „мІҙлҘј лӢӨмӢң мҙҲкё°нҷ” н•ҙм•јн•ҳлҜҖлЎң 1м§Җ мҠӨнӮ¬мқ„ л¶ҷмқҙлҠ”лҚ° л“ңлҠ” 비мҡ©мқ„ нҸ¬н•Ён•ҙм„ң лӢӨмӢң мІҳмқҢл¶Җн„° мӢңмһ‘н•ҙм•јн•ҳмЈ . (лҚңлҚңлҚң..)
н—¬л Ҳл„Ө м„ңлІ„м—җм„ң к·ёл Ҳмқҙл“ңмҷҖ к°•нҷ”м—җ лјҲлҘј л¬»кі кі„мӢ мқҳмІңлҸ„лӢҳмқҳ мһҗл¬ёмңјлЎң 1м§Җ, 2м§Җ, 3м§Җм—җ л“ңлҠ” к°Ғк°Ғмқҳ 비мҡ©мқ„ к°Ғк°Ғ В 1м–ө, В 2м–ө, В 5м–өмңјлЎң мһЎм•ҳмҠөлӢҲлӢӨ. В к·ёлҰ¬кі н•Ёмһ¬кё° к°ҖкІ©мқ„ 1.5м–өмқҙлқјкі мһЎкі кі„мӮ°н•ҙліҙм§Җмҡ”. лӢӨн–үнһҲлҸ„ мң„мқҳ мӢқмқ„ ліёлӢӨл©ҙ 2м§ҖмҷҖ 3м§ҖлҠ” н•ҳлӮҳлЎң 묶м–ҙм„ң кі„мӮ°н•ҙлҸ„ кҙңм°®мҠөлӢҲлӢӨ. мҰү, 1м§Җм—җ л“ңлҠ” 비мҡ©мқҙ 1м–ө, 3м§Җм—җ л“ңлҠ” 비мҡ©мқҙ 7м–ө мқҙл ҮкІҢл§Ң кі„мӮ°н•ҙлҸ„ лі„ л¬ём ңк°Җ м—ҶкІ кө°мҡ”. Analyticн•ҳкІҢ кі„мӮ°н•ҙлҸ„ л‘җ мӮ¬кұҙмқҙ мһҗмІҙм ҒмңјлЎң лҸ…лҰҪмӮ¬кұҙмқҙкё° л•Ңл¬ём—җ лі„ л¬ём ңк°Җ м—Ҷм§Җл§Ң, мқҙн•ҙлҘј лҸ•кё° мң„н•ҙм„ң Monte Calro Simulationмқ„ лҸҢл Өліҙкё°лЎң н•ҳм§Җмҡ”.В
мӢӨм§Ҳм Ғмқё мҳҲ
л¬јлЎ к·ёл Ҳмқҙл“ңлҠ” л°°м—җ л”°лқјм„ң м–ҙл–Ө мҳөмқҙ л¶ҷм–ҙм•ј н•ҳлҠ”м§Җ лӢӨ лӢӨлҘҙм§Җл§Ң, (м—¬кё°м„ң кө°л°°лҠ” мҳҲмҷёлЎң н•©лӢҲлӢӨ. м ңк°Җ н•ҳлӮҳлҸ„ лӘЁлҘҙкё°м—җ..) м—¬кё°м„ңлҠ” 1м§Җм—җлҠ” к°Җк°•, мҠӨ추лҘј л…ёлҰ¬кі , 3м§Җм—җлҠ” к°Җк°•2, мҠӨ추2лҘј л…ёлҰ°лӢӨкі н•©мӢңлӢӨ.В к·ёл Ҳмқҙл“ң мҳөм…ҳмҠӨнӮ¬лЎң л¶ҷмқ„ мҲҳ мһҲлҠ” мҠӨнӮ¬мқҳ мҲҳлҠ” В мҙқ к°•нҷ”мҲҳм№ҳ : лӮҙкө¬, м„ёлЎңлҸӣ, к°ҖлЎңлҸӣ, мЎ°л Ҙ, м„ нҡҢ, лӮҙнҢҢ, мһҘк°‘, м„ мӢӨ, нҸ¬мӢӨ, м°Ҫкі В м¶”к°Җліҙл„ҲмҠӨ : к°ҖмҶҚк°•нҷ”, м„ мҲҳнҸ¬, м„ мёЎнҸ¬, м„ лҜёнҸ¬, мҠӨнӮ¬м¶”к°Җ, мҠӨнӮ¬мҠ№кі„В к°ңмЎ°ліҙл„ҲмҠӨ : нҸ¬н•Ёк°ңмЎ°, мһҘк°‘н•Ёк°ңмЎ°, л°ұлі‘н•Ёк°ңмЎ°, нғҗмӮ¬м„ к°ңмЎ°
к°•нҷ”мҲҳм№ҳ (10к°ң) + 추к°Җліҙл„ҲмҠӨ (6к°ң) + к°ңмЎ°ліҙл„ҲмҠӨ (4к°ң) мһ…лӢҲлӢӨ. В В мқҙмӨ‘м—җм„ң мһ„мқҳлЎң м ңмҷён• мҲҳ мһҲлҠ” мҳөл“ӨмқҖ мЎ°л Ҙ : лІ”м„ м—җлҠ” л¶ҷм§Җ м•ҠмқҢ м„ мёЎнҸ¬ : мқҙлҜё 5мҠ¬лЎҜмқҙл©ҙ л¶ҷм§Җ м•ҠмқҢ к°ңмЎ°ліҙл„ҲмҠӨ : 2к°• мғҒнғңлЎң мҠӨнӮ¬мқҙ н’Җмқҙл©ҙ л¶ҷм§Җ м•ҠмқҢ к·ёлҹ¬л©ҙ 20к°ң мӨ‘м—җм„ң 6к°ңлҘј м ңмҷён•ҳл©ҙВ
14к°ңмқҳ мҠӨнӮ¬мӨ‘м—җм„ң н•ңк°ңк°Җ лһңлҚӨмңјлЎң л¶ҷлҠ” кұ°л„Өмҡ”. м—ӯмӢң мһҗл¬ёмқ„ кө¬н•ң мқҳмІңлҸ„лӢҳмқҳ мқҳкІ¬м—җ л”°лҘҙл©ҙ, мқҙ мҠӨнӮ¬мқҙ л¶ҷлҠ” нҷ•лҘ мқҖ pure randomмқҙл©° м–ҙл–Ө к°ҖмӨ‘м№ҳ(Weight)лҠ” мЎҙмһ¬н•ҳм§Җ м•ҠлҠ”кІғ к°ҷлӢӨкі н•©лӢҲлӢӨ. (л¬ҙмҠЁ л§җмқёк°Җн•ҳл©ҙ мҠӨнӮ¬мқҳ probability function p(x)лҠ” uniformн•ҳлӢӨлҠ” мқҙм•јкё°мқёлҚ°мҡ”.. мқҙлҠ” мқҙнӣ„мқҳ мӢң뮬л Ҳмқҙм…ҳм—җм„ң мӨ‘мҡ”н•ң мқҳлҜёмқҙлҜҖлЎң..)
мқҙмӨ‘м—җм„ң мҠӨнӮ¬ мҠ№кі„ м—ӯмӢң л…јмҷёлЎң л‘ЎлӢҲлӢӨ. кі„мӮ°н•ҳл Өл©ҙ лӘ»н•ҳлҠ” кІғлҸ„ м•„лӢҲм§Җл§Ң, мҠӨнӮ¬ мҠ№кі„лҠ” м• мҙҲм—җ м–ҙл–Ө лӘ©м Ғмқ„ к°Җм§Җкі м ңл¬јл°°лҘј мӮ¬мҡ©н•ҙм•ј н•ҳлҜҖлЎң к·ёл Ҳмқҙл“ң 비мҡ©мһҗмІҙк°Җ 비м•Ҫм ҒмңјлЎң мҰқк°Җн•ҳкі (м ңл¬ј л°°к°’мқҙ мӣ”л“ұнһҲ 비мҢҲ) лҳҗн•ң 1м§Җм—җ мҠӨнӮ¬ мҠ№кі„к°Җ лңЁм§Җ м•Ҡмңјл©ҙ л°Җм–ҙлІ„л Өм•ј н•ҳлҜҖлЎң ліёл¬ём—җм„ң кі„мӮ°н•ҳлҠ” мқјл°ҳм Ғмқё кёҖл“ңмһ‘мқҳ м Ғм •к°ҖкІ©кіј кұ°лҰ¬к°Җ лЁј мқҙм•јкё°к°Җ лҗ мҲҳ мһҲкІ л„Өмҡ”.
к·ёлҹј к°ҖмһҘ мү¬мҡҙ к°ңмЎ°лЎұмқҳ кІҪмҡ° мқёлІӨмқҳ "мҠӨнҺҳмқёкөӯмҷ•" лӢҳк»ҳм„ң мқҙлҜё к·ёл Ҳмқҙл“ңмӢң мқҳлҜёмһҲлҠ” мҳөм…ҳмқ„ м •лҰ¬н•ҙ мЈјм…ЁмңјлҜҖлЎң (м¶ңмІҳ "http://www.inven.co.kr/board/powerbbs.php?come_idx=498&query=view&p=1&my=&category=&sort=PID&orderby=&where=&name=subject&subject=&content=&keyword=%B1%D7%B7%B9%C0%CC%B5%E5&sterm=&iskin=&mskin=&l=14396") м•„мЈј к°„лӢЁн•ҳкІҢ кі„мӮ°н•ҙліјк№Ңмҡ”? мқјлӢЁ к°ңмЎ°лЎұм—җкІҢ мқҳлҜёмһҲлҠ” мҳөм…ҳмқҖ к°Җк°•, мҠӨ추, м„ мӢӨ, м°Ҫкі мқҙл ҮкІҢ 4к°ң лҝҗмқёкұ° к°ҷл„Өмҡ”. л¬јлЎ мһ‘м—…мғҒ 1м§Җм—җ к°Җк°•мқҙ лӮҳмҳӨм§Җ м•Ҡмңјл©ҙ м°ЁлқјлҰ¬ л°Җм–ҙлІ„лҰ¬кі , лӢӨмӢң мӢңмһ‘н•ҳмӢңкІ м§Җл§Ң, кө¬мһ…н•ҳлҠ” мӮ¬лһҢмқҳ мһ…мһҘм—җм„ңлҠ” к°Җк°• мҠӨ추лӮҳ, мҠӨ추 к°Җк°•мқҙлӮҳ л§Ҳм°¬к°Җм§ҖмқҙлҜҖлЎң к·ёлғҘ мӢң뮬л Ҳмқҙм…ҳмқ„ лҸҢл Өліҙкё°лЎң н•ҳмЈ .
В мӢң뮬л Ҳмқҙм…ҳм—җм„ңлҠ” нҸ¬мӢӨ, м„ мӢӨмқҖ л‘җлІҲл¶ҷм§Җ м•ҠлҠ”лӢӨлҠ”кұё к°җм•Ҳн•ҙм„ң кі„мӮ°н–ҲмҠөлӢҲлӢӨ.В
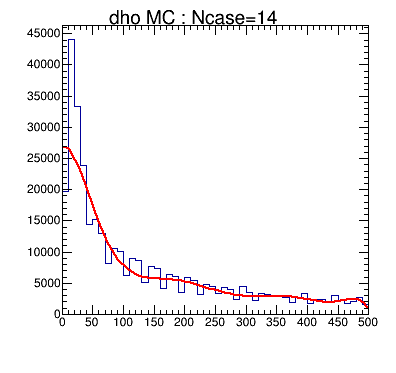
мң„ Plotмқ„ ліҙл©ҙ мһ¬лҜёмһҲлҠ”кІҢ, м •к·ң분нҸ¬(Gausian)кіј лӢ¬лҰ¬ кј¬лҰ¬к°Җ л№ лҘҙкІҢ м—Ҷм–ҙм§Җм§Җ м•ҠлҠ”лӢӨлҠ” кІҒлӢҲлӢӨ. Tailмқҳ мЎҙмһ¬- мҰү , м•„л¬ҙлҰ¬ нҡҹмҲҳк°Җ лҠҳм–ҙлӮҳлҸ„ мҳҒмӣҗнһҲ мӣҗн•ҳлҠ” мҳөм…ҳмқ„ к°–м§Җ лӘ»н• нҷ•лҘ мқҙ мЎҙмһ¬н•ңлӢӨлҠ” кұ°м§Җмҡ”..(м•„л§Ҳ лӮң м•Ҳлҗ кәјм•ј..) мқҙлҹҙ кІҪмҡ° мқҙ functionмқ„ Fitн•ҙм„ң кұ°кё°м„ңмқҳ RMS мҷҖ кё°лҢҖлҗҳлҠ” Sigma к°’мқ„ 추м¶ңн• мҲҳ мһҲмҠөлӢҲлӢӨ. мң„ к°ҷмқҙ Tailмқҙ мЎҙмһ¬н•ҳлҠ” 분нҸ¬лҠ” Landauн•ЁмҲҳлЎң fitмқ„ н•ҳл©ҙ мһҳ л§һкІҢ лҗҳм§Җмҡ”.
FitмқҖ нҷ•лҘ мқҳ кі„мӮ°мқём җмқ„ к°җм•Ҳн•ҳм—¬ Chi-SquareлҢҖмӢ Likelihood л°©лІ•мңјлЎң кі„мӮ°н–Ҳкі к·ё кІ°кіјлҠ” лӢӨмқҢкіј к°ҷмҠөлӢҲлӢӨ.В MEAN В 9.018e+00 В sigma2 В 6.781e+00 FCN=879.474 FROM MIGRAD В В STATUS=CONVERGED В В В 83 CALLS В В В В В 84 TOTAL В В В В В В В В В В В EDM=5.33758e-06 В В STRATEGY= 1 В В В ERROR MATRIX ACCURATE В EXT PARAMETER В В В В В В В В В В В В В В В В В STEP В В В В FIRST В NO. В В В В VALUE В В В В В В ERROR В В В В В SIZE В В В DERIVATIVE В В 1 В В В 1.54863e+05 В 2.03265e+03 В 7.22193e+00 В -1.45227e-06 В В 2 В В В В В 1.57886e+00 В 1.90170e-01 В 6.79859e-04 В 1.69990e-03 В В 3 В В В В 4.13512e+00 В 2.13140e-02 В 1.42350e-05 В 3.81260e-01
к·ёл ҮлӢӨл©ҙ мқјлӢЁ Mean к°’мқ„ ліјк№Ңмҡ”?В нҸүк· к°’ 9м—җм„ң +- 6 м—җм„ң Sigma level 2 мңјлЎң мҲҳл ҙн•ҳлҠ” кө°мҡ”.В мӮ¬мӢӨ Landauн•ЁмҲҳмқҳ нҠ№м§• мһҗмІҙлҘј ліҙл©ҙ мқҙмғҒн• кІҢ м—ҶлҠ” кІ°кіјмһ…лӢҲлӢӨ. (мқҳмҷёлҠ” 9м—җм„ң 6.7мқ„ л№јлҸ„ В 2.3мқёлҚ°, мҷң 2к°Җ нҸ¬н•Ёлҗҳм§Җ м•Ҡм•ҳлҠ”м§Җ, 2м—җм„ңл§Ң 8%м •лҸ„мқёлҚ°... м•„л§Ҳ мқҙлҠ” histogramмқҖ discrete н•ҳкі , fucntionмқҖ continuousн•ҙм„ң мғқкё°лҠ” л¬ём ң к°ҷкё°лҠ” н•©лӢҲлӢӨл§Ң..) м•„л¬ҙнҠј мҳҲмғҒн•ңлҚ°лЎң лӮҳмҷ”л„Өмҡ”.В мҰү 14к°ңмӨ‘м—җм„ң 4к°ңмқҳ мҠӨнӮ¬мқ„ мӣҗн• л•Ң, нҸүк· 9лІҲм •лҸ„мқҳ мҙҲкё°нҷ” кіјм •мқ„ кұ°м№ҳл©ҙ мӣҗн•ҳлҠ” 2мҠӨнӮ¬мқҙ л¶ҷмқҖ л°°лҘј кө¬н• мҲҳ мһҲмҠөлӢҲлӢӨ. лҳҗн•ң мҡҙмқҙ м—ҶлҚ”лқјлҸ„ 9+6.7 (мҰү 15лІҲ~16лІҲ) м •лҸ„ мһ¬мӢңлҸ„лҘј н•ҳл©ҙ 2sigmaм—җ н•ҙлӢ№н•ҳлҠ” 95.45%мқҳ нҷ•лҘ лЎң мӣҗн•ҳлҠ” л°°лҘј кө¬н• мҲҳ мһҲмҠөлӢҲлӢӨ. мқҙ кіјм •мқҙ мқҙн•ҙк°Җ м•ҲлҗҳмӢңлҠ” 분мқҖВ http://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule м—¬кё°лҘј м°ёмЎ°н•ҳм„ёмҡ”.
кҙҖмӢ¬мһҲм–ҙн• кІ°кіј
к·ёлҹ°лҚ° м–ҙм ң мқҳмІңлҸ„лӢҳкіј лҢҖнҷ”лҘј н•ҳл©ҙм„ң, мң м Җ분л“ӨмқҖ мқҙлҹ° 분нҸ¬м—җлҠ” лі„ кҙҖмӢ¬мқҙ м—Ҷкі , кІ°көӯ мӨ‘мҡ”н•ңкұҙ "к·ёлҹј мӣҗк°Җк°Җ м–јл§Ҳл©ҙ лҗңлӢӨлҠ” кұ°лғҗ!!!!" лҚ”кө°мҡ”..В
к·ёлһҳм„ңВ к·ёл ҮлӢӨл©ҙ мң„мқҳ мӢқм—җ лҢҖмһ…н•ҙм„ң н•ңлІҲ кі„мӮ°н•ҙліҙл©ҙ, мӢң뮬л Ҳмқҙм…ҳмңјлЎңл¶Җн„° 1лІҲм§ё мһҳлӘ»лҗҳм–ҙ мһ¬мӢңлҸ„н•ң к°’кіј 2лІҲм§ё мһҳлӘ»лҗҳм–ҙ мһ¬мӢңлҸ„н•ң к°’мқ„ parameterлЎң л¶Ҳлҹ¬мҷҖм„ң кі„мӮ°н•ҙлҙ…лӢҲлӢӨ.В В мһ‘업비мҡ© В = В (((1м§Җ) * ((N_1 * н•Ёмһ¬кё°)+1)) + (2м§Җ) + (3м§Җ)) * ((N_2 *н•Ёмһ¬кё°)+1))В В мқҙ кІҪмҡ°м—җлҠ” лҚ” мүҪмҠөлӢҲлӢӨ. к·ёлғҘ лғ…лӢӨ fitн•ҳкі м Ғ분н•ҳл©ҙ лҗҳлӢҲк№Ңмҡ”. statitical errorлҠ” нҡҹмҲҳк°Җ мҰқк°Җн•ҳл©ҙ м•Ңм•„м„ң мӨ„м–ҙл“Өкәјкі , binning effectлҘј кі л Өн•ҙм„ң м Ғ분мӢң histogramкіј weightлҘј л°ҳл°ҳ мЈјл©ҙ к№”лҒ”н•ң м Ғ분мқҙ к°ҖлҠҘн•©лӢҲлӢӨ.В
к·ёлһҳм„ң лӘҮк°Җм§Җ кІҪмҡ°мқҳ мҲҳмҷҖ к·ё мӣҗк°Җнҷ•лҘ (мқҙлқјкі н•ҙм•јн•ҳлӮҳлҘј кіөк°ңн•©лӢҲлӢӨ.) 1. 12к°ңмқҳ кІҪмҡ°мқҳ мҲҳ мӨ‘м—җм„ң м—°мҶҚм ҒмңјлЎң 1к°ң мӣҗн•ҳлҠ” мҠӨнӮ¬мқҙ л¶ҷмқ„ л•Ңмһ…лӢҲлӢӨ. (1/12 + 1/12 В : В ex)к°Җк°• 1 + к°Җк°• 2) нҷ•лҘ мқҖ В 50м–ө л“Өм—¬м„ң л¶ҷмқј нҷ•лҘ : В 8.621 100м–ө л“Өм—¬м„ң л¶ҷмқј нҷ•лҘ : 13.0004 200м–ө л“Өм—¬м„ң л¶ҷмқј нҷ•лҘ : 18.6566
2. лӢӨмқҢмқҖ 14к°ңмқҳ мҠӨнӮ¬мӨ‘м—җм„ң мһ„мқҳмқҳ 1мҠӨнӮ¬ к·ёлҰ¬кі лӢӨмқҢм—җ 14к°ңмӨ‘м—җм„ң мһ„мқҳмқҳ 2мҠӨнӮ¬мқҙ л¶ҷмқ„ нҷ•лҘ мһ…лӢҲлӢӨ. ( 1/14 + В 2/14 : В к°Җк°• + мҠӨ추 В or к°Җк°• +к°Җк°• ) 50м–ө л“Өм—¬м„ң л¶ҷмқј нҷ•лҘ : В 27.0894 100м–ө л“Өм—¬м„ң л¶ҷмқј нҷ•лҘ :В 38.5186 200м–ө л“Өм—¬м„ң л¶ҷмқј нҷ•лҘ : 51.3506
л¬јлЎ лӮҳлҠ” к°Җк°• 12 мҷём—җлҠ” лӢӨ н•„мҡ”м—Ҷм–ҙ лқјкі н•ҳл©ҙ м Ғм •к°ҖкІ©мқҖ кё°н•ҳкёүмҲҳм ҒмңјлЎң мҳ¬лқјк°‘лӢҲлӢӨ.
л¬јлЎ мқҙкІғмқҖ нҷ•лҘ лЎңл§Ң кі„мӮ°н•ң мӣҗк°Җмһ…лӢҲлӢӨ. м—¬кё°м—җ мЎ°м„ кіөлӢҳмқҳ мҲҳкі +мӢңк°„+л©ҳнғҲмқ„ к°җм•Ҳн•ҳл©ҙ +/- к°Җ нҸ¬н•Ёлҗҳм–ҙм•ј кІ м§Җмҡ”. к·ёлғҘ н• мқј м—Ҷм–ҙм„ң, кі„мӮ°кё°лҘј л‘җл“ңл Өліё кІ°кіјмһ…лӢҲлӢӨ. :) Post Script. нҳ№мӢңлӮҳ 200м–өмқ„ л¶Җм–ҙлҙӨмһҗ кІЁмҡ° 18%лқјлӢҲ!! лқјлҠ” мқҳкІ¬м—җ мқҳмӢ¬мқ„ н’ҲлҠ” 분л“Өмқ„ мң„н•ҙм„ң мўҖлҚ” м—°мһҘлҗң plotмқ„ мІЁл¶Җн•©лӢҲлӢӨ. (1000м–өк№Ңм§Җ..) ліҙмӢңл©ҙ м•„мӢңкІ м§Җл§Ң, Landau tailмқ„ gausn мІҳлҹј л№ лҘҙкІҢ 0мңјлЎң мҲҳл ҙн•ҳлҠ”кІҢ м•„лӢҲлқјм„ңмҡ”..В
EXP
34,033
(34%)
/ 36,001
|
|
|




 thdnice
thdnice 










